سیستم مختصات
سیستم مختصات یکی از مفاهیم بسیار مهم در جغرافیا است که پایه تمام نقشهها و محاسبات مکانی است که ریشه در علم هندسه دارد. در هندسه، یک سیستم مختصات یک سیستم است که از یک یا چند عدد و یا مختصات برای تعریف منحصر به فرد موقعیت نقاط و یا سایر عناصر هندسی روی یک خمینه (manifold) مانند فضای اقلیدسی، استفاده میکند. ترتیب عناصر مختصات مهم است و گاهی توسط موقعیت خود در یک تاپل مرتب شده و گاهی توسط یک حرف مانند x-coordinate شناسایی میشوند. مختصات در ریاضیات ابتدایی اعداد حقیقی محسوب میشوند، اما ممکن است اعداد مختلط و یا عناصر یک سیستم انتزاعیتر مانند حلقه جابهجایی باشند. کاربرد سیستم مختصات اجازه میدهد مسائل هندسی به مسائل عددی ترجمه شوند و بالعکس؛ که این اساس هندسه تحلیلی است.
سیستمهای مختصات رایج
مختصات خطی
سادهترین مثال از یک سیستم مختصات تعیین نقاط بر روی یک خط با اعداد حقیقی توسط محور اعداد است. در این سیستم، یک نقطه دلخواه O (مبدا) روی محور انتخاب میشود. مختصات یک نقطه P توسط فاصله علامتدار (مثبت یا منفی) از نقطه O تا نقطه P تعریف میشود. مثبت یا منفی بودن فاصله بستگی به این دارد که P در کدام سمت مبدا قرار گرفته باشد. هر نقطه یک مختصات یکتا گرفته و هر عدد حقیقی مختصات یک نقطه یکتا است.

مختصات خطی و محور اعداد
سیستم مختصات دکارتی
نمونه رایج یک سیستم مختصات، سیستم مختصات دکارتی است. در صفحه، دو محور عمود بر هم انتخاب شده و مختصات یک نقطه، فاصله علامتدار تا محورها در نظر گرفته میشود.
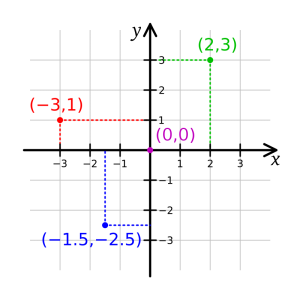
سیستم مختصات دکارتی
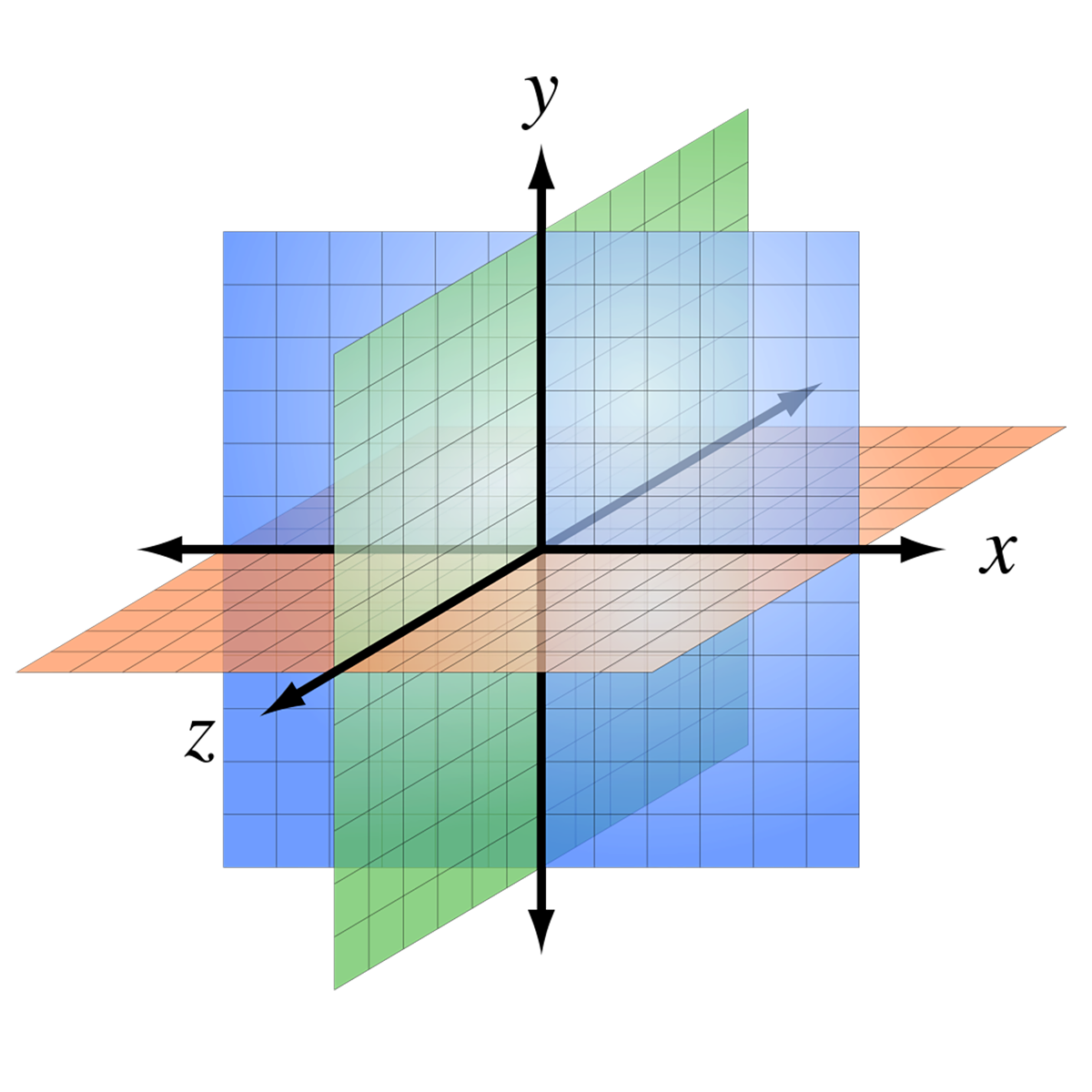
در سه بعد، سه صفحه عمود بر هم انتخاب شده و سه مختصات یک نقطه، فواصل علامتدار از هر یک از صفحات است. این را میتوان برای تولید n مختصات برای هر نقطهای در فضای اقلیدسی n صفحهای تعمیم داد.
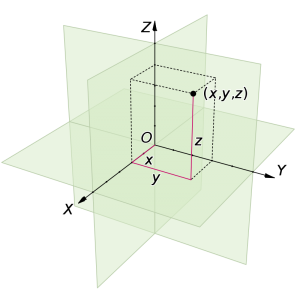
سیستم مختصات دکارتی 3 بعدی
سیستم مختصات قطبی
یکی دیگر از سیستمهای مختصات رایج، سیستم مختصات قطبی است. یک نقطه به عنوان قطب انتخاب شده و یک شعاع از آن به عنوان محور قطبی در نظر گرفته میشود. در یک زاویه مشخص (θ) تنها یک خط از قطب میگذرد که زاویه آن با محور قطبی θ (تتا) باشد (به صورت پادساعتگرد محاسبه میشود). در نتیجه تنها یک نقطه یکتا بر روی این خط وجود دارد که فاصله علامتدار آن از قطب r باشد. برای یک جفت مختصات (r, θ) تنها یک نقطه وجود دارد، ولی هر نقطه توسط جفتهای متعددی از مختصات میتواند تعریف شود. برای مثال، (r, θ)، (r, θ+2 π) و (-r, θ+ π) همگی مختصات قطبی یک نقطه مشابه است. مختصات (0, θ) نیز برای هر مقداری از θ بیانگر قطب است.
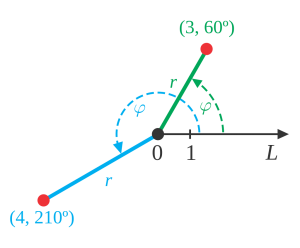
سیستم مختصات قطبی
سیستم مختصات استوانهای و کروی
دو روش معمول برای توسعه سیستم مختصات قطبی به سه بعد وجود دارد. در سیستم مختصات استوانهای، یک مختصات z با معنای مشابه در مختصات دکارتی به r و θ در مختصات قطبی اضافه میشود که یک سهگانه (r, θ, z) را تشکیل میدهد. بدین شکل که r و θ در قاعده یک استوانه و z در ارتفاع آن تعریف میشوند.
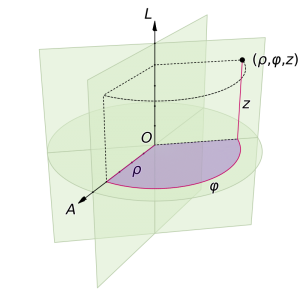
سیستم مختصات استوانهای
سیستم مختصات کروی یک گام جلوتر رفته و یک جفت از مختصات سهگانه استوانهای (r, z) را به مختصات قطبی تبدیل کرده است که یک مختصات سهگانه (ρ, θ, φ) تشکیل میدهند. در این سهگانه ρ (رو) معادل r در سیستم مختصات قطبی است، θ (تتا) نیز مشابه سیستم قطبی است که زاویه گِرایی یا آزیموت نامیده میشود و φ (فی) زاویه از سمت الراس (زنیت) است که زاویه سمت الراسی نامیده میشود.
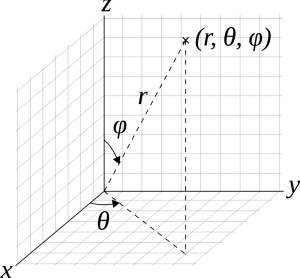
سیستم مختصات کروی
سیستم مختصات جغرافیایی
یک سیستم مختصات جغرافیایی یک سیستم مختصات است که تعریف هر مکان بر روی کره زمین را با مجموعهای از اعداد، حروف و یا نمادها ممکن میسازد. این مختصات اغلب به گونهای انتخاب میشود که هر یک عدد بیانگر موقعیت عمودی و دو یا سه عدد بیانگر موقعیت افقی باشد؛ از سوی دیگر، یک موقعیت جغرافیایی ممکن است با یک مختصات مرکب سه بعدی بردار دکارتی بیان شود. یکی از اشکال معمول مختصات عرض جغرافیایی (Latitude)، طول جغرافیایی (Longitude) و ارتفاع است.
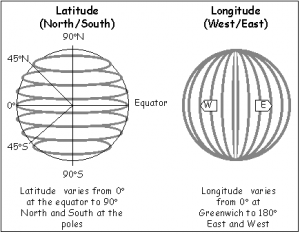
طول و عرض جغرافیایی
برای اطلاع بیشتر پیرامون سیستم مختصات جغرافیایی پیشنهاد میکنم مقاله بیضوی مرجع (بیضوی مبنا) چیست؟ را بخوانید.
منابع




هنوز دیدگاهی برای این مطلب ثبت نشده است.